1522. Оптимальное бинарное дерево поиска
Рассмотрим
множество S = {e1, e2, …, en}, состоящее из n
различных элементов таких, что e1
< e2 < … < en. Рассмотрим бинарное
дерево поиска, состоящее из элементов S. Чем чаще производится запрос к
элементу, тем ближе он должен располагаться к корню.
Стоимостью cost доступа к элементу ei
из S в дереве будем называть значение cost(ei), равное числу ребер на
пути, который соединяет корень с вершиной, содержащей элемент. Имея частоту
запросов к элементам из S, (f(e1), f(e2), ..., f(en)),
определим общую стоимость дерева следующим образом:
f(e1) * cost(e1) + f(e2) * cost(e2)
+ … + f(en) * cost(en)
Дерево, имеющее наименьшую
стоимость, считается наилучшим для поиска элементов из S. Именно поэтому оно
называется Оптимальным Бинарным Деревом Поиска.
Вход. Состоит из нескольких тестов, каждый из которых
расположен в отдельной строке. Первое число в строке n (1 ≤ n ≤
250) указывает на размер множества S. Следующие n неотрицательных целых чисел описывают частоты запросов элементов
из S: f(e1), f(e2), ..., f(en) (0 ≤ f(ei) ≤ 100).
Выход. Для каждого
теста в отдельной строке вывести стоимость Оптимального Бинарного Дерева
Поиска.
|
Пример
входа |
Пример
выхода |
|
1 5 3 3 1 7 7 4 10 6 2 3
5 7 6 1 3 5 10 20 30 |
0 5 49 63 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Представьте, что
Вы написали программу перевода слов и выложили в интернет. Слова раположены в
вершинах бинарного дерева.
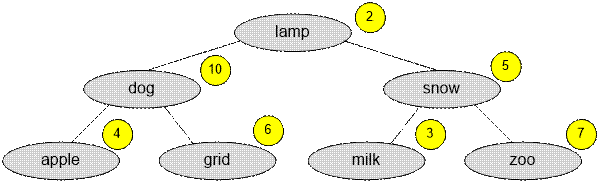
Через некоторое
время для каждого слова ei (ключ) Вы узнали количество запросов f(ei) к нему. Значения f(ei) обозначим желтым цветом. Стоимость текущего Дерева
Поиска равна
10 + 4 * 2 + 6
*2 + 5 + 3 * 2 + 7 * 2 = 55
Возникает
вопрос: можно ли изменить структуру дерева так, чтобы минимизировать указанную стоимость?
Для указанного
примера Оптимальное Бинарное Дерево Поиска имеет вид:
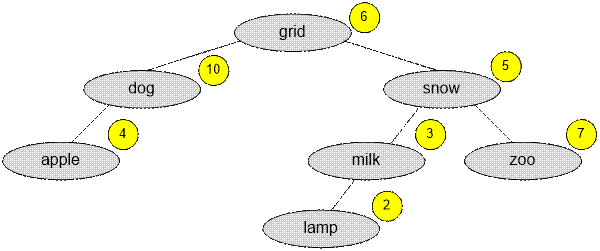
Его стоимость
равна
10 + 4 * 2 + 5 +
3 * 2 + 7 * 2 + 2 * 3 = 49
Пусть Ti,j равно стоимости
оптимального бинарного дерева поиска,
которое можно построить из элементов ei,
ei+1, …, ej. Очевидно, что Ti,i = 0 (стоимость дерева поиска из одной вершины равно нулю). Для
i < j имеет место рекуррентность:
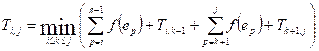
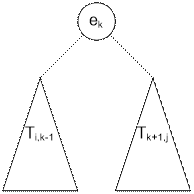
Элемент ek
ставим в корне. Стоимость построения левого поддерева равна Ti,k-1, правого Tk+1,j. При этом
поскольку корень левого поддерева находится на один уровень ниже ek,
то для учета стоимости левого поддерева необходимо добавить сумму частот всех
его элементов, то есть значение ![]() . Аналогично при подсчете стоимости правого поддерева следует
прибавить
. Аналогично при подсчете стоимости правого поддерева следует
прибавить ![]() .
.
При i > j
положим Ti,j
= 0.
Отметим также,
что решение задачи про оптимальное бинарное дерево поиска аналогично решению
задачи про оптимальное умножение матриц.
Пример
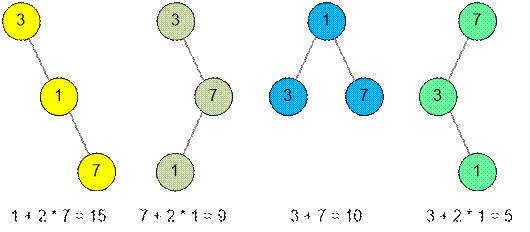
стоимости деревьев
На рисунках изображены не все возможные деревья, но
отметим, что правое крайнее дерево будет оптимальным, его стоимость наименьшая
среди всех возможных и равна 5.
Рассмотрим
четвертый тест. Искомое оптимальное бинарное дерево поиска имеет вид:
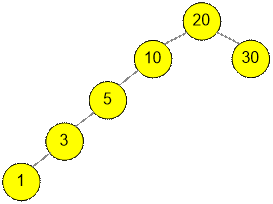
Тогда

Стоимость левого
поддерева (если бы 10 было корнем):
T1,4
= 5 + 3 * 2 + 1 * 3 = 14
Стоимость
правого поддерева (если бы 30 было корнем): T6,6 = 0.
Если при k = 5 достигается указанный минимум, то
![]() = (1 + 3 + 5 + 10) +
14 + (30) + 0 = 63,
= (1 + 3 + 5 + 10) +
14 + (30) + 0 = 63,
что равно
стоимости всего дерева.
Реализация алгоритма
Объявим константы.
#define MAX 300
#define
INF 0x3F3F3F3F
Объявим рабочие массивы.
int m[MAX], sum[MAX];
int t[MAX][MAX];
Входные частоты
элементов храним в массиве m, в массиве sum будут храниться
частичные суммы частот: sum[i] = ![]() . Значения Ti,j будут раниться в массиве t.
. Значения Ti,j будут раниться в массиве t.
Частичная сумма ![]() возвращается функцией weight(i, j).
возвращается функцией weight(i, j).
int weight(int
i, int j)
{
if (i > j)
return 0;
return sum[j]
- sum[i-1];
}
Функция go(i, j) возвращает значение
Ti,j.
int go(int
i, int j)
{
if (i > j)
return 0;
if (t[i][j]
== INF)
{
for (int k = i; k <= j; k++)
{
int temp
= go(i,k-1) + go(k+1,j) + weight(i,k-1) + weight(k+1,j);
if (temp
< t[i][j]) t[i][j] = temp;
}
}
return
t[i][j];
}
Основная часть
программы. При считывании частот элементов устанавливаем t[i][i] = Ti,i = 0. Остальные значения
ячеек массива t устанавливаем равными бесконечности.
while(scanf("%d",&n)
== 1)
{
memset(t,0x3F,sizeof(t));
for(i = 1; i
<= n; i++)
{
scanf("%d",&m[i]);
t[i][i] = 0;
}
Вычисляем частичные суммы массива m.
sum[0] = 0
for(i = 1; i
<= n; i++)
sum[i] = sum[i-1] + m[i];
Вычисляем
значение T1,n вызовом
go(1, n). Выводим ответ.
go(1,n);
printf("%d\n",t[1][n]);
}
Java реализация
import java.util.*;
public class Main
{
static int t[][],
sum[];
static int
weight(int i, int j)
{
if (i >
j) return 0;
return sum[j] - sum[i-1];
}
static int go(int i, int j)
{
int k, temp;
if (i >
j) return 0;
if (t[i][j] == Integer.MAX_VALUE)
{
for (k = i; k
<= j; k++)
{
temp = go(i,k-1) +
go(k+1,j) + weight(i,k-1) +
weight(k+1,j);
if (temp <
t[i][j]) t[i][j] = temp;
}
}
return t[i][j];
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
while(con.hasNextInt())
{
int n = con.nextInt();
t = new int[n+1][n+1];
for(int i = 1;
i <= n; i++)
Arrays.fill(t[i], Integer.MAX_VALUE);
int m[] = new int[n+1];
sum = new int[n+1];
for(int i = 1;
i <= n; i++)
{
m[i] = con.nextInt();
t[i][i] =
0;
}
sum[0] =
0;
for(int i = 1;
i <= n; i++)
sum[i] = sum[i-1] +
m[i];
go(1,n);
System.out.println(t[1][n]);
}
con.close();
}
}